|
 |
In the bubble sort, as elements
are sorted they gradually
"bubble" (or rise) to their proper location in the array, like bubbles rising in a glass of soda.
The bubble sort
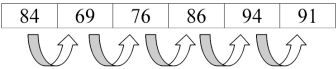
repeatedly compares adjacent elements of an
array. The first and second elements are compared and swapped if out of
order. Then the second and third elements are compared and swapped
if out of order. This
sorting process continues until the last two elements of the array are
compared and swapped if out of order.
|
|
When this first pass through the array is complete, the bubble sort returns to
elements one and two and starts the process all over again. So, when
does it stop? The bubble sort knows that it is
finished when it examines the entire array and no "swaps" are needed
(thus the list is in proper order).
The bubble sort keeps track of the occurring swaps by the use of
a flag.
The table below follows an array of numbers before, during, and after a
bubble sort for descending order. A "pass" is defined as one
full trip through the array comparing and if necessary, swapping,
adjacent elements. Several passes have to be made through the array
before it is finally sorted.
|
| Array at beginning: |
84 |
69 |
76 |
86 |
94 |
91 |
| After Pass #1: |
84 |
76 |
86 |
94 |
91 |
69 |
| After Pass #2: |
84 |
86 |
94 |
91 |
76 |
69 |
| After Pass #3: |
86 |
94 |
91 |
84 |
76 |
69 |
| After Pass #4: |
94 |
91 |
86 |
84 |
76 |
69 |
| After Pass #5 (done): |
94 |
91 |
86 |
84 |
76 |
69 |
The bubble sort is an easy algorithm to program, but it is slower than many
other sorts. With a bubble sort, it is always necessary to make one final
"pass" through the array to check to see that no swaps are made to ensure
that the process is finished. In actuality, the process is finished before
this last pass is made.
// Bubble Sort Method for Descending Order
public static void BubbleSort( int [ ] num )
{
int j;
boolean flag = true;
// set flag to true to begin first pass
int temp;
//holding variable
while ( flag )
{
flag= false; //set flag to false
awaiting a possible swap
for( j=0;
j < num.length -1; j++ )
{
if ( num[ j ] < num[j+1] ) // change to
> for ascending sort
{
temp = num[ j ];
//swap elements
num[ j ] = num[ j+1 ];
num[ j+1 ] = temp;
flag = true; //shows a swap occurred
}
}
}
}
Remember that a
bubble sort will continue until no swaps have occurred,
meaning that the array is in the proper sorted order. |