|
Solving Rational/Fractional Equations
Rational (or fractional) equations can be solved by:
| |
1. determining the least common denominator (LCD) for the problem,
2. multiplying both sides of the equation by the LCD (multiply ALL terms),
3. solving the resulting equation, and
4. checking for possible extraneous roots since the derived equation may not
be equivalent to the original equation. |
The graphing calculator is a wonderful back-up checking tool to solving such equations. It is especially helpful in determining extraneous roots. Note the examples below:
Example 1: Solve the following equation algebraically and check.
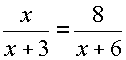
Algebraic Solution:
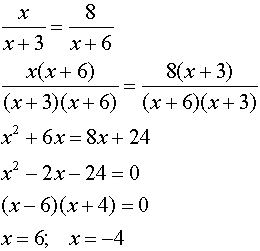
|
Graphical check:
Enter the left side of the equation into f1(x).
Enter the right side of the equation into f2(x).
Be careful to include the parentheses for entering the denominators in this problem.
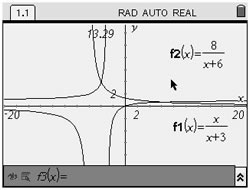
Use the INTERSECT option.
MENU - #6 Points & Lines
#3 Intersecting point(s)
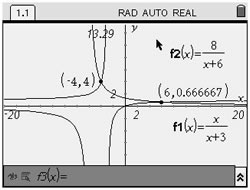
Checking the two intersection points, gives:
( -4,4) and ( 6, 2/3)
|
Check:
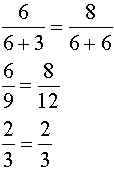 |
Check:
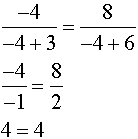 |
Both roots check in this problem. Notice that the graph shows TWO intersection points. |
| |
| Example 2: Solve the following equation algebraically and check.
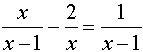
Algebraic Solution:
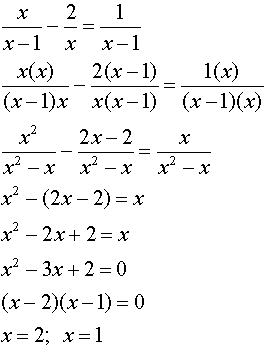 |
Graphical check:
Enter the left side of the equation into f1(x).
Enter the right side of the equation into f2(x).
Be careful to include the parentheses for entering the denominators in this problem.
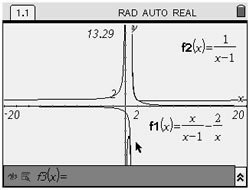
Since so much activity is occurring around the origin, the next screen shows a "Zoom in".
Use the INTERSECT option.
MENU - #6 Points & Lines
#3 Intersecting point(s)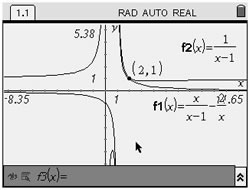
A "Zoom box" near x = 1 shows there is not intersection point at x = 1.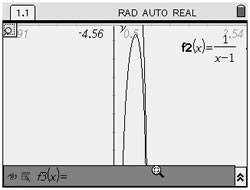
|
Check:
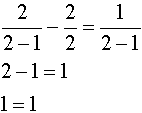 |
Check:
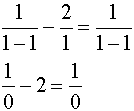
Division by zero is undefined. x = 1 is NOT an answer.
x = 1 is an extraneous root. |
|
Hint: When working with rational equations, it may be difficult to "see" the intersection point if the viewing window is a small representation of the graph. You may want to enlarge the viewing window by adjusting the WINDOW settings or by using ZOOM. You can always quickly return to the standard viewing window by choosing option #5 from the WINDOW menu.
Remember: In Example 2, you can see that there is only one answer to the equation since there is only one point of intersection. Should there be NO points of intersection, the answer will be the empty set.
|


![]()