Are the asymptotes really there?

Asymptotes - Am I Really Seeing Them?

When graphing various trigonometric functions on the TI-83+ and TI-84+ (with OS prior to V2.40),
it may appear that asymptotes are also being graphed. Are these really asymptotes?
(ANSWER: No. They are not asymptotes.)

NOTE: Starting with the TI-84+ Operating System V 2.40, this problem no longer exists.

Let's examine some trigonometric graphs in Radian MODE:

Graph y = tan(x)

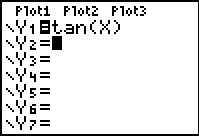
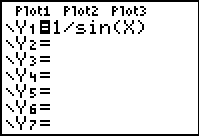
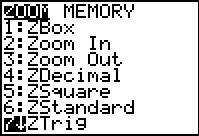
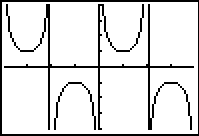
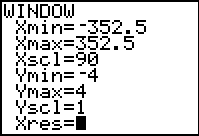
Enter the function. Set the MODE to Radian. Choose ZOOM #7 ZTrig

The Graph

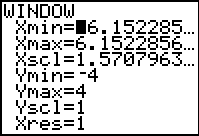
Window in ZTrig

The same graph in DOT mode. No asymptotes!!

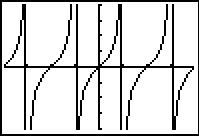
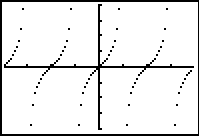
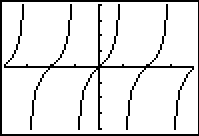
These vertical lines are not the asymptotes. They are simply the calculator behaving as it should in "Connected" mode -- it is "connecting" the points.

Graph y = csc(x)

This same problem occurs with the graph of
y = csc(x)
in Radian MODE.

Enter the function.

Graph using ZOOM #7 ZTrig

BUT.... If I use DEGREE MODE, I don't see these "supposed" asymptotes. Why??

Let's examine these same two functions in DEGREE Mode. y = tan (x) y = csc (x) Still in connected mode.	Set the mode to Degree	Window in ZOOM #7 ZTrig
y = tan(x)	y = csc(x)	Notice -- there are NO "supposed" asymptotes, or "heartbeat" lines, in these graphs.

So, why am I not seeing "heartbeat" lines in Degree mode?

The answer can be found by examining the windows created by ZTrig.

RADIAN - ZTrig

DEGREE - ZTrig

Note: The Degree Mode uses 90 as the Xscl.
The Radian Mode does not truly use as Xscl. It expresses this value as an approximate decimal.

The Radian Mode window does not truly use as Xscl.
It expresses this value as an approximate decimal.

In Radian mode, the calculator is never graphing the undefined points on the graphs. The decimal approximations for these locations are slightly "off" -- meaning that the graph is not undefined at these "close" approximations and consequently points are plotted. When a point is plotted, the connected mode engages and connects adjacent points.

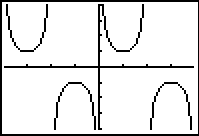
The Degree Mode window uses 90 as the Xscl.

In Degree mode, the calculator attempts to graph the actual undefined points. Such an attempt produces an "error" and nothing is plotted for those x-values. Consequently, a break in the graph appears (a non-plotting), preventing the connected mode from connecting adjacent points, which prevents the creation of the "heartbeat" line.

Finding Your Way Around TABLE of CONTENTS