Solving Quadratic Equations Using Calculator Functions TI-Nspire

Solving Quadratic Equations - Special Features
There are a couple of "Special Calculator Functions" that can be used to solve quadratic equations,
or find the factors of quadratic expressions.

The first "special feature" is the "nSolve" function.
This function is used to find numerical solutions to quadratic equations,
or to find factors of the quadratic expressions.

If there is more than one solution to an equation (such as in the case of a quadratic equation with 2 solutions), this function will list the smallest of the solutions only. You will need to "encourage it" to give you the other solutions.

The format for nSolve is to enter the equation, followed by a comma, and then state the variable.
You can add a "guess" after the variable, but it is optional, You could use "guess" to check your guess for the missing solution.

Using Numerical Solve, nSolve(), to solve a quadratic equation
(or determine factors) .

Solve: x² - x - 12 = 0

1. Start a new Document: Calculator

2. We can activate nSolve() by
• , #3 Algebra, #1 Numerical Solve

or
• from the Catalog (if you need format info)

3. Enter the equation: nSolve(x² - x - 12 = 0, x)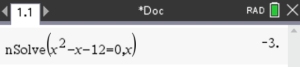
nSolve() only shows ONE answer for a quadratic.
We know quadratics can have 2 roots, 1 repeated root, or no real roots (complex conjugates).

4. How to get the other unique solution, if there is one:
The second real root will either be "greater than" or "less than" the stated answer of -3.

Let's test and see what happens:
Copy that previous entry again, followed by the "such that" symbol ( | ) and x < -3.

nSolve(x² - x - 12 = 0,x) | x < -3

The yellow warning triangle is telling us that it is giving a questionable result. In this case, it is not finding a root less than -3.

So, the missing root must be greater than -3.
nSolve(x² - x - 12 = 0,x) | x > -3

ANSWERS: x = -3, x = 4
If factoring, the factors are (x + 3) and (x - 4).

CATALOG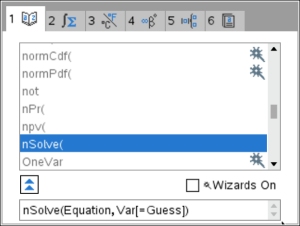
Choose tab 1 for an ABC listing.
Arrow down to the word you want.
Typing the first letter will jump down the list.

If you are not familiar with how to type the format for this feature, the catalog will show you what is needed at the bottom of the screen.
The format shows an optional [Guess].
The guess is not needed.

To get the "such that" vertical bar symbol

to get the Inequality Template:

When appears,
clicking on the symbol will
give a broad indication of the error.

Alternative Access for nSolve:
type: x² - x - 12 = 0 Pause

#2 Math Actions,
#1 Solve Numerically

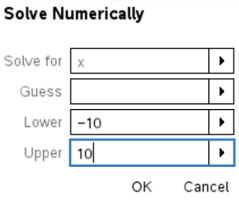
If you are uncertain, choose a wider range.
Hit OK,

Follow the steps on the left for finding the second root,

The second "special feature" is the "Polynomial Tools" set of functions.

There are three functions within this category:
1. Find Roots of Polynomials
2. Real Roots of Polynomials
3. Complex Roots of Polynomials
These commands can help you solve a quadratic equation
or help you factor a quadratic expression.

Let's see how these options may apply.

2.	1. Using Find Roots of Polynomials, to solve a quadratic equation (or determine factors).
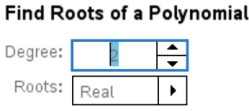
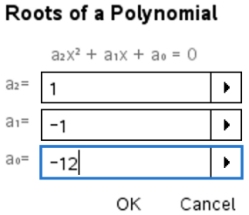
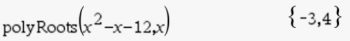
	Solve: x² - x - 12 = 0 Let's take another look with a different function. 1. Start a new Document: Calculator 2. We can activate nSolve() by • , #3 Algebra, #3 Polynomial Tools 3. Choose #1: Find Roots of Polynomial For quadratics: Degree 2, Roots Real OK 4. Enter coefficients of quadratic. 5. View the solutions: ANSWERS: x = -3, x = 4 If factoring, the factors are (x + 3) and (x - 4).	Alternative Access for Find Roots of Polynomial: Enter the quadratic expression (no equal sign): type: x² - x - 12 Pause #1 Math Actions, #1 Find Roots of Polynomial
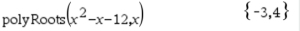
	2. Using Real Roots of Polynomials, to solve a quadratic equation (or determine factors).
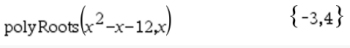
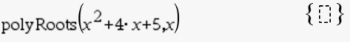
	This option will automatically set the choice of roots to "Real". Note: If you enter an equation such as x² + 4x + 5 = 0, you will get: a set of curly braces around an empty box. The cause is that you entered an equation whose roots are "complex", and not "Real". So there are NO Real answers. You need to use option #3 Complex Roots of Polynomials.

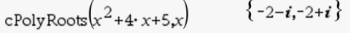
What about equations with complex roots?

1. Using Find Roots of Polynomials, to solve a quadratic equation.

Solve: x² - 2x + 5 = 0
(from the previous page)

Be sure you calculator settings are set to COMPLEX.
, #5 Settings, #2Document Settings
Real or Complex: Rectangular
("Rectangular" implies Complex)

1. Start a new Document:

2. , #3 Algebra, #3 Polynomial Tools

3. Choose #1: Find Roots of Polynomial For quadratics: Degree 2 Roots Complex OK

4. Enter the coefficients of the quadratic:

5. View the solutions in terms of i: 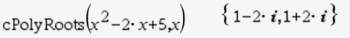ANSWER: 1 - 2i and 1 + 2i (conjugate pair) If factoring, the factors are (x - (1 - 2i)) and (x - (1 + 2i))

3. Using Complex Roots of Polynomials, to solve a quadratic equation.

This option will automatically set the choice of roots to "Complex":

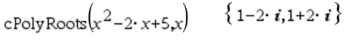
If you don't know if the roots will be "Real" or "Complex", use this "Complex" option.

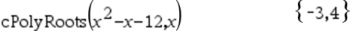
This option will return "Complex" roots if the equation is a complex quadratic equation AND it will return "Real" roos if the equation is a real quadratic equation.

Remember that the Real Numbers are a subset of the Complex Numbers making the use of "Complex" all inclusive.

Sometimes the answer will be "messier", as was the last example in the previous lesson.

Using Find Roots of Polynomials, to solve a quadratic equation.

Solve: x² - 3x + 9 = 0
(from the previous page)

Be sure you calculator settings are set to COMPLEX
, #5 Settings, #2Document Settings
Real or Complex: Rectangular

1. Start a new Document:

2. , #3 Algebra, #3 Polynomial Tools

3. Choose #1: Find Roots of Polynomial For quadratics: Degree 2, Roots Complex OK

4. Enter the coefficients of the quadratic:

5. View the solutions in terms of i:

We saw in the calculation at the last lesson, that the answer was . You can see by the check below that the answers are equivalent,

CAS version: The CAS version of the calculator will have
additional capabilities for theses functions, TBA

Table of Contents | MathBits.com | Terms of Use
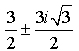