MathBits.com Table of Contents

Solving Quadratic Inequalities

Working with quadratic inequalities is similar to working with linear inequalities.
(See Linear Inequalities and Inequality Graphing)

Consider the following examples:

S I N G L E    V A R I A B L E:

1. Solve:  
 

1.  Enter the left side of the inequality into Y1.
2.  Enter the right side of the inequality into Y2.
3.  Enter the inequality into Y3 using the inequality symbols found under 2nd MATH (TEST).  Remember the Y1 and Y2 are found under Vars →Y-VARS, #1Function. 
4.  Hit GRAPH.

Just as we saw in Linear Inequalities, a small bar appears representing the graph of the value 1, showing where the inequality is true.  In this case, the inequality is true for  2 < x < 5.  To determine the "exact" values for the endpoints, use the INTERSECT option (2nd TRACE (CALC) #5 intersect) with Y1 and Y2.

Looking at the table shows that the Y3 values alternate between being a 0 (false) and a 1 (true).
(Arrow to the right to "see" the column for Y3.

Remember that < will not "include" the endpoints.





 

G R A P H S:

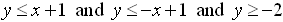
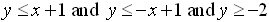
2. Graph:  
 

1.  Set
2.  Arrow to the far left of the equal sign and hit ENTER until the "greater than" symbol appears.  If you go past it, keep hitting ENTER, as it will come around again.
3.  Hit GRAPH.

Remember, when working with inequalities on the graphing calculator, YOU must decide if the graph (in this case the parabola) is drawn as a dotted or solid entity.  The graph is solid if the equation includes "equal to".  This graph would be drawn solid.

 



 

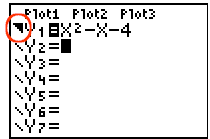
3. Graph the system:  Only One Root?
  Solve:  

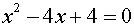
When graphed, this equation only intersects the x-axis in one location.  This tells you that this root repeats itself.   

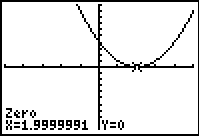If a reading appears such as 1.9999991, the actual answer is most likely the number 2.  Check your assumption that the answer is 2 by substituting 2 into the original equation to see if it satisfies the equation.

Standard 10 x 10 window

 

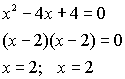4. What if the graph does not intersect the x-axis???
(or intersect option shows no intersections)
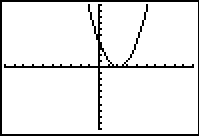
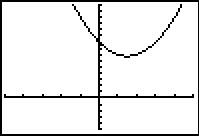
  Solve: 

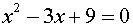
When graphed, this equation does NOT intersect the x-axis.  This tells you that the roots of this equation are complex values.  Dig out the quadratic formula to find the roots.

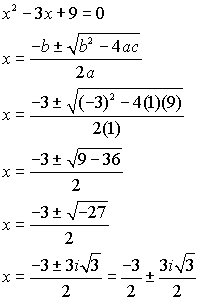Window [-5,5] x [-5,15]

 

 

 

5. Need to WRITE a quadratic equation from a graph?
  If you are given the visual graph of a quadratic equation and you are given or can identify at least 3 points, you can use the Quadratic Regression process to create the equation of the graph.

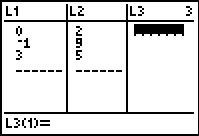
Write the equation of the parabola shown at the right, given that the points (0,2), (-1,9) and (3,5) are on the graph.

1.  Enter the points into L1 and L2 (x-coordinate in L1 and matching y-coordinate in L2)
(See Basic Commands for Stats if you need more assistance.)

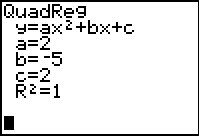
2.  Press STAT.  Arrow over to CALC.  Choose #5 QuadReg.

3.  On the home screen:  QuadReg L1, L2

4.  Press ENTER.  You will see the screen at the right showing you the coefficients of the quadratic equation.
This equation is
                      

 



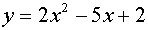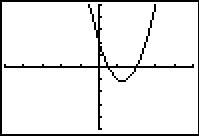
Finding Your Way Around TABLE of CONTENTS