Table of ContentsMathBits.com
Conics

Graphing Circles
 
A.  center at the origin:
      		B.  center at (h, k):
   

Example A:  Graph:  
 

Solution:
  • Enter the equation into Y= by solving for y.
     
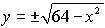
  • Enter the positive square root into Y1.
  • Enter the negative square root into Y2, or enter the negation of Y1.
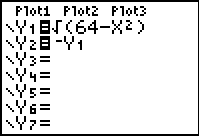
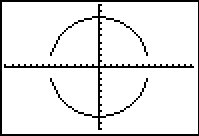
  • If you choose ZOOM #6 (the standard window), the graph will appear to be an ellipse rather than a circle due to the 3/2 aspect ratio of the viewing screen (the standard viewing screen is not a square).
  • Choose ZOOM#5 ZSquare to create a viewing window where the units on both axes are the same length.
 
 

 


 


 

 

 

 

 

 

 

NOTE: 
* You may notice that the "vertical" edges of the graph will not appear in the viewing window.  The viewing screen cannot graph points that fall between pixels.
* Since the positive and negative square roots were graphed as two separate equations, the TRACE function will not move smoothly between the two sections of the graph.  The up arrow can be used to move between the two sections of the graph.  The cursor will disappear if it is moved beyond the domain for which x is defined. 
 

 

 
  E Q U A T I O N S:

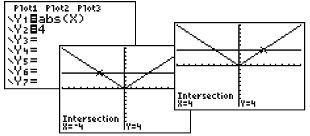
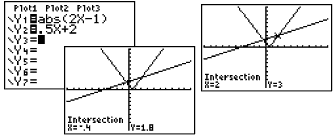
Example 1:     Solve:  

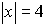
  • Enter left side in Y1.  You can find abs( ) quickly under the CATALOG (above 0)
    ( or MATH → NUM, #1 abs( )

  • Enter right side in Y2

  • Use the Intersect Option (2nd CALC #5) to find where the graphs intersect.  Move the spider near the point of intersection, press ENTER.  Simply hit ENTER twice more.  You must repeat this process to find the second point of intersection.

  • Answer:  x = 4;  x = -4

                                                    
Example 2:    Solve: 
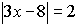
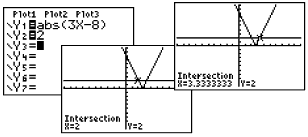
  • Answer:  x = 2;  x = 3.3333333
    The x value is stored in the calculator's memory.  If you wish to change 3.333333333 to a fraction, simply return to the home screen, hit x, hit Enter.  Now, change to fraction. (2nd MATH, #1►Frac )
    Answer:  x = 2;  x = 10/3
 
Example 3:    
       Solve: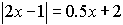 
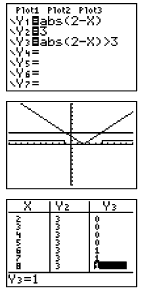
  • Answer:  x = -.4;  x = 2
 
 
  I N E Q U A L I T I E S:

Example 4:    Solve: 

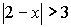
Boolean Check:     

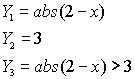(The inequality symbols are under
the TEST Menu - 2nd MATH.)
 

Answer:  x < -1;  x > 5
You could also enter 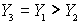       ( using Y1 and Y2  found under
                                                                                       Vars →Y-Vars, Function)

Where the inequality is true, y-values on the graph will be a 1.

If you look at the table, 0's will be listed where the inequality is false and 1's will be listed where the inequality is true. 

Determine exact cut off points by using the intersection option.  Remember that the calculator cannot draw an open or closed circle on the intervals.  You will have to determine which circle is needed based upon whether the inequality includes "equal to".   Find the endpoints by using the intersect option (2nd TRACE #5 intersect).

If you turn off the axes (FORMAT - 2nd ZOOM), you will be able to see the graphing of the 0's and 1's more clearly.  Notice that the small vertical segment connecting the 0's to the 1's is simply the calculator being set in "connected" mode.  Change to "dot" mode to remove this segment.

 
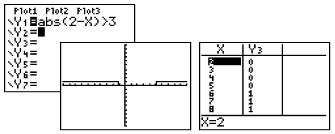
You "can" enter the inequality directly.  Since you will not have the two graphs from which to determine the intersection points, you will  need to examine the table to determine the exact value of the open/closed endpoints.

 

Example 5:   Solve:  
Algebraic solution:
                             
Answer:  The values that make the compound inequality true are
                                .

Calculator solution:  (inequality expression is entered using "and")
                           [and can be found quickly under the CATALOG (above 0) -
                                           or TEST (2nd MATH)→LOGIC, #1 and]


Different table settings can be used to examine the data:



BACK