|
A logarithm is an
exponent.
|
As this example shows, 3 is the
exponent to which the base 2 must be raised to create the answer of 8,
or 23 = 8. In general terms:
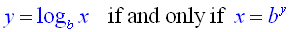
(where x > 0 and
b is a positive constant
not equal to 1) |
|
BASE 10: Logarithms with base 10 are called common logarithms.
When the base is not indicated, base 10 is implied.
The log key on the
graphing calculator will calculate the
common (or base 10) logarithm.
2nd log will calculate the antilogarithm or 10x
 |
|
|
OTHER BASES:
|
|
You can also hit ALPHA (key), WINDOW
and choose
the fifth option on the menu, logBASE(.
|
|
|
BASE e:
Logarithms with base e are called natural logarithms.
Natural logarithms are denoted by ln.
On the graphing calculator, the base e logarithm is the ln key.
|
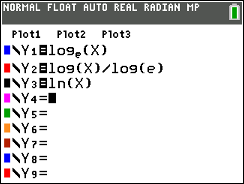
All three are the same. |
|
When working with logarithms on your graphing calculator,
you must
remember the "Change of Base Formula":
|
|
Remember, the notation:
log x is with respect to base 10
ln x is with respect to base e |
Examples:
|