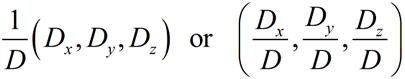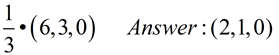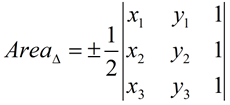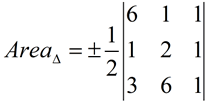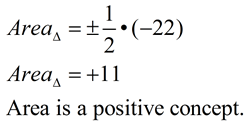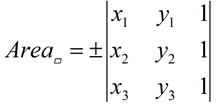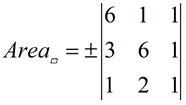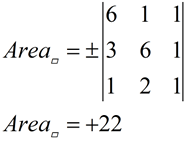|

|
Working with Determinants
|
|
Applications of Determinants |
Solving Systems of Equations |
A process called Cramer's Rule uses determinants to solve small systems of linear equations.
When the system is 2x2 or 3x3, with a unique solution, Cramer's Rule may be used to arrive at the solution.
Let's see how Cramer's Rule applies to a 2x2 system:
1.
Solve this 2x2 system of equations using
Cramer's Rule:
|
2y + 3x = -1
4 = 2x - y |
Re-write so the variables and constants are lined up:
3x + 2y = -1
2x - y = 4
The "x-variable coefficients"
are
3, 2.
The "y-variable coefficients"
are 2, -1.
The "constants" are -1, 4. |
Set up Cramer's Rule: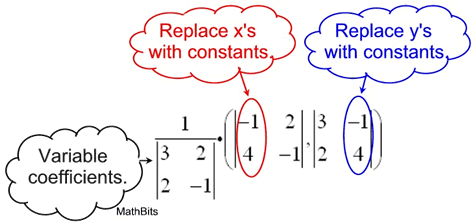 The variable coefficients "line-up" as you see them lined-up in the system.
The variable coefficients "line-up" as you see them lined-up in the system. |
Did you notice how Cramer's Rule is set up?
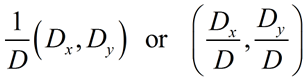
• The rule is "one" over a determinant formed by the coefficients of the variables from the system (D),
• multiplied by an "ordered pair" of determinants (using that same determinant of the coefficients with a couple of replacements).
•
The first determinant in the "ordered pair" (Dx) has its x-column replaced by the "constants" from the system, and
•
the second determinant in the "ordered pair" (Dy) has its y-column replaced by the "constants" from the system. |
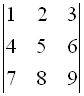
| Use the graphing calculator to solve these 2x2 determinants to find the solution to this system. |
Evaluate the three determinants as shown at the top of this page:
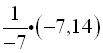 Answer: (1,-2) Answer: (1,-2) |
Beware!! When using Cramer's Rule, if the value of the variable coefficient determinant, D, is zero, division by zero will occur. This is why Cramer's Rule specifies a "unique solution", meaning one, actual solution. In this 2x2 situation, if division by zero occurs, it means that the solution to the system will either not exist (the lines are parallel) or the solution set will be infinite (the lines coincide, one on top of the other). |
Let's see how Cramer's Rule applies to a 3x3 system:
2. Solve this 3x3 system of equations using Cramer's Rule:
|
x + 2y - z = 4
x + y + z = 3
2x + y + z = 5 |
The variable are already lined up and ready to go.
x + 2y - z = 4
x + y + z = 3
2x + y + z = 5
|
Set up Cramer's Rule: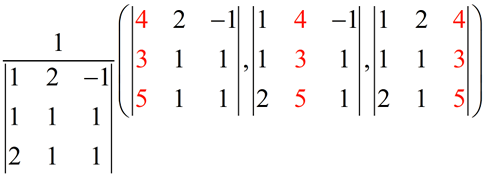 Notice how the x column, then the y column and finally the z column are each replaced by the constants in the ordered triple determinants.
Notice how the x column, then the y column and finally the z column are each replaced by the constants in the ordered triple determinants. |
Notice that the set up for this 3x3 system is the same concept we saw in the 2x2 system. We are working with an "ordered triple" in this problem, instead of an "ordered pair". We simply have more variables with which to work in this problem.
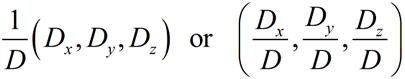
|
| Use the graphing calculator to solve these 3x3 determinants to find the solution to this system. |
Evaluate the three determinants as shown at the top of this page:
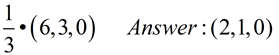 |
Beware!! Remember if the value of the variable coefficient determinant, D, is zero, division by zero will occur. In this 3x3 situation, this means that the solution to the system will either not exist (the planes are parallel) or the solution set may be infinite (the planes intersect in a line, not a point). |
Finding Area in Coordinate Geometry |
Now, let's take a look at another application of determinants. This time we will look at applications to coordinate geometry.
3. Find the area of a triangle with vertices A(6,1), B(1,2), and C(3,6).
Formula: The area of a
triangle having vertices (x1,y1),
(x2,y2), and (x3,y3)
is:
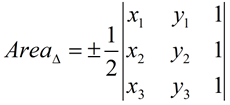
|
Substitute values:
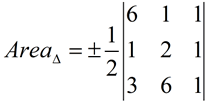 |
Calculate the answer:
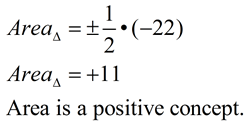 |
| This formula contains "±" to ensure that the answer for area is a positive concept. Depending upon the order in which the points are arranged in a determinant, the determinant may yield a negative result. This does not mean the numerical component of the answer is incorrect - it simply has a negative sign. To avoid a negative answer for area, the "±" reminds you to state the answer as positive. |
4. Find the area of a parallelogram with vertices A(6,1), B(3,6), C(1,2), and D(4,-3).
| Since a parallelogram can be divided into two congruent triangles by drawing a diagonal, the area of the parallelogram can be found by simply removing the ½ from the formula for the area of a triangle. We will retain the "±" to again be sure that the area is listed as positive. If you are given all four vertices of the parallelogram, you can find the area by using ANY of the three points. |
Formula: The area of a
parallelogram having 3 of its vertices at (x1,y1),
(x2,y2), and (x3,y3)
is:
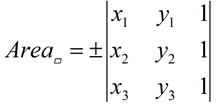 |
Substitute values:
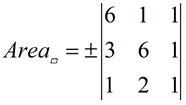
Using points A, B and C. |
Calculate the answer:
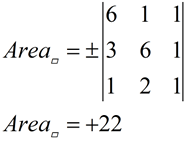 |
|








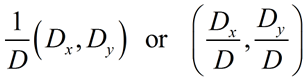
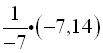 Answer: (1,-2)
Answer: (1,-2)