|
The exchange sort is similar to
its cousin, the bubble sort, in that it compares elements of the array and swaps those that are
out of order.
(Some people refer to the "exchange sort" as a "bubble sort".) The difference between these two
sorts is the manner in which they compare the elements. The exchange sort compares the first element with
each following element of the array, making any necessary swaps.
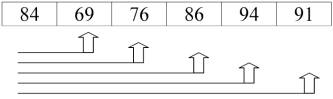 |
When the first pass through the array is complete, the
exchange sort then takes the second element and compares it with each
following element of the array swapping elements that are out of order.
This sorting process continues until the entire array
is ordered.
Let's examine our same table of elements again using an
exchange sort for descending order. Remember, a "pass" is defined as one full
trip through the array comparing and if necessary, swapping elements
| Array at beginning: |
84 |
69 |
76 |
86 |
94 |
91 |
| After Pass #1: |
94 |
69 |
76 |
84 |
86 |
91 |
| After Pass #2: |
94 |
91 |
69 |
76 |
84 |
86 |
| After Pass #3: |
94 |
91 |
86 |
69 |
76 |
84 |
| After Pass #4: |
94 |
91 |
86 |
84 |
69 |
76 |
| After Pass #5 (done): |
94 |
91 |
86 |
84 |
76 |
69 |
The exchange sort, in some situations, is slightly more efficient than the
bubble sort. It is not necessary for the exchange sort to make that final
complete pass needed by the bubble sort to determine that it is finished.
//Exchange Sort Method for Descending Order
public static void ExchangeSort ( int [ ] num )
{
int i, j, temp; // be sure the temp variable is same "type" as the array
for ( i = 0; i < num.length - 1; i ++ )
{
for ( j = i + 1; j <
num.length; j ++ )
{
if(
num[ i ] < num[ j ] ) // sorting into descending order
{
temp = num[ i ]; // swapping
num[ i ] = num[ j ];
num[ j ] = temp;
}
}
}
}
When completed, the array will be
in descending order and can be printed from main.
For
ascending order, change the
" if " inequality to >.