One
of the skills which is useful to programmers is an understanding of
the relationship between number bases. When you understand how
numbers are represented in base two
(Binary),
base eight (Octal),
and base sixteen (Hexadecimal), you will better understand references which will be made later in this course.
The
number system that we all know and love is the Decimal number system, base 10. In our number system we utilize the digits
0, 1, 2, 3, 4, 5, 6, 7, 8, and 9. All numbers are formed by
combining these digits.
Other
number bases work in the same manner only with different digits.
The Binary number system, base 2, uses only the digits 0 and 1.
The Octal number system, base 8, uses the digits 0, 1, 2, 3, 4, 5, 6, and 7.
The Hexadecimal number system, base 16, uses the
digits and letters 0, 1, 2, 3, 4, 5, 6, 7, 8, 9, A, B, C, D, E, and
F.
Notice how, in each of these number systems, the number of digits
contained within the system is the name of the system. Base 2 has 2
digits, Base 10 has 10 digits, and so on. Just be careful to
remember that each system starts counting with 0.
Each
system uses its digits to form all of the numbers contained within
the system. In the number system that we know and love, base 10, we
are familiar with the terms ones, tens, hundreds, thousands, etc.
used to describe the position a digit holds within a number. These
terms are actually words that describe powers of 10.
The positions within a number in base 10 are formed by
systematically raising the number 10 to various powers.
| 100 = 1 |
(ones) |

|
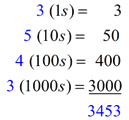 |
| 101 = 10 |
(tens)
|
| 102 = 100 |
(hundreds) |
| 103 = 1000 |
(thousands) |
The
same process is used to create numbers in other number systems as
well. The only difference is that instead of raising 10 to a power,
the new base number is used. For example, when working in base 8,
you are working with powers of 8 (80, 81, 82,
83, ...). Base 2 works with powers of 2, base 16 works
with powers of 16, and so on.
In our study of computer programming, most of our
references will be made to the binary number system. The simplicity
of only dealing with two digits (0 or 1) is very appealing to a
computer system. The 0 and 1 can represent current being turned OFF
or ON. Notice how switches on computer hardware often display a 0
or a 1 to represent off or on.
The power symbol:
Toggle power switches contain a "0" and a "1" to universally indicate "Off" or "On".
A single on/off button contains a combination of the "0" and
the "1" as shown at the right. |
|
Now,
let's go on to the next lesson page and look at
how to convert from
one number base to another.
|